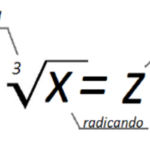Contradição no Raciocínio Lógico: Conceitos e Exemplos
No contexto da lógica proposicional, a contradição ocorre quando uma proposição resulta sempre falsa, independentemente da veracidade de suas partes constituintes. Em termos formais, uma contradição é uma fórmula proposicional que nunca pode ser verdadeira.
O que é uma Contradição?
Uma contradição é uma proposição que possui a forma P ∧ ¬P, ou seja, uma afirmação e sua negação sendo verdadeiras ao mesmo tempo, o que é impossível dentro dos princípios da lógica clássica. Como consequência, qualquer argumento que tenha uma contradição como premissa é inválido, pois leva a qualquer conclusão arbitrária (princípio do explosion, ou ex falso quodlibet).
Exemplos de Contradição
- Exemplo Simples:
- Premissa 1: “Todos os gatos são pretos” (P).
- Premissa 2: “Existe pelo menos um gato que não é preto” (¬P).
- Essas duas premissas juntas formam uma contradição, pois não podem ser verdadeiras simultaneamente.
- Exemplo Matemático:
- Suponha que temos a equação x = 2 e ao mesmo tempo x ≠ 2.
- Não há valor de x que satisfaça ambas as proposições, tornando o sistema contraditório.
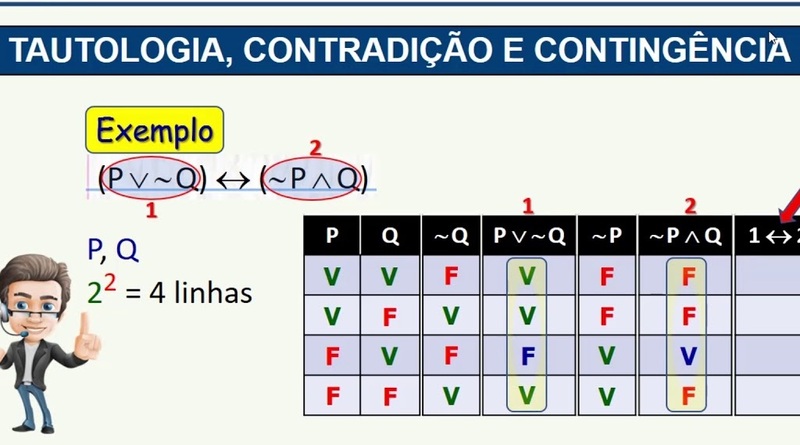
- Exemplo na Lógica Formal:
- Considere a fórmula (P ∧ ¬P).
- Sua tabela-verdade mostrará que essa proposição é sempre falsa, independentemente do valor de P.
Consequências da Contradição
Na lógica clássica, a contradição tem sérias implicações:
- Princípio da Não Contradição: Nada pode ser verdadeiro e falso ao mesmo tempo.
- Princípio do Explosion: Se uma contradição for assumida como verdadeira, qualquer proposição pode ser inferida a partir dela.
- Importância na Lógica e na Matemática: Evitar contradições é fundamental para a validade de demonstrações matemáticas e sistemas formais.
Como Evitar Contradições?
- Verificar a consistência das premissas antes de construir um argumento.
- Utilizar métodos formais como tabelas-verdade ou provas por contradição para identificar falhas.
- Adotar sistemas lógicos alternativos, como a lógica paraconsistente, que permite o tratamento de contradições sem levar ao colapso lógico.
Conclusão
A contradição no raciocínio lógico é um conceito fundamental para a coerência dos argumentos e sistemas formais. Seu estudo é essencial para a filosofia, matemática e ciências da computação, ajudando a estruturar um pensamento lógico e consistente.