Número de Linhas de uma Tabela-Verdade: Como Calcular e Exemplos

A tabela-verdade é uma ferramenta fundamental na lógica proposicional, usada para analisar todas as possíveis combinações de valores verdadeiros e falsos de proposições. Ela tem aplicações em matemática, filosofia, eletrônica digital e ciências da computação. Um dos aspectos mais importantes ao construir uma tabela-verdade é determinar quantas linhas ela terá. Neste post, vamos explorar como calcular esse número e exemplificar seu uso na prática.

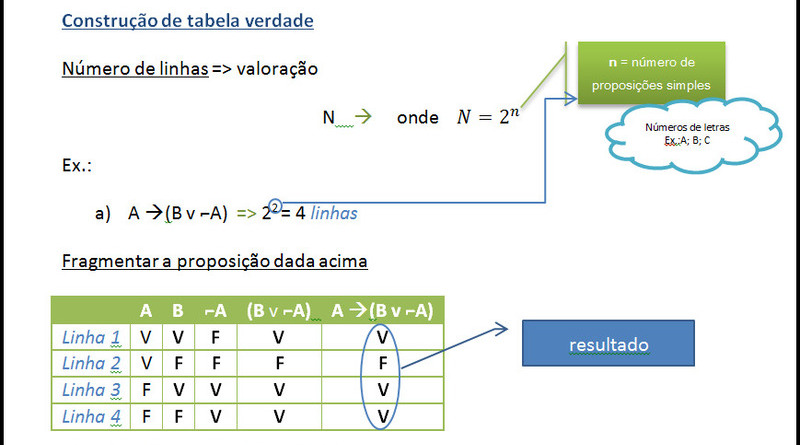
Como Calcular o Número de Linhas

O número de linhas de uma tabela-verdade depende do número de proposições (ou variáveis lógicas) envolvidas. Para um conjunto de n proposições distintas, a fórmula para determinar o número de linhas é:

L = 2ⁿ

Isso ocorre porque cada proposição pode assumir dois valores: verdadeiro (V) ou falso (F). Assim, para n proposições, todas as possíveis combinações desses valores são dadas por 2ⁿ.

Exemplos Práticos

Vamos aplicar a fórmula a alguns casos:

• 1 proposição (n = 1): L = 2¹ = 2
  

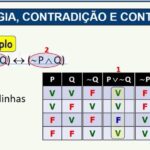
  P
  V
  F

• 2 proposições (n = 2): L = 2² = 4
  

  P	Q
  V	V
  V	F
  F	V
  F	F

• 3 proposições (n = 3): L = 2³ = 8
  

  P	Q	R
  V	V	V
  V	V	F
  V	F	V
  V	F	F
  F	V	V
  F	V	F
  F	F	V
  F	F	F

À medida que o número de proposições aumenta, o total de linhas cresce exponencialmente. Por exemplo, para 4 proposições, teríamos  2⁴ = 16 linhas, para 5 proposições, 2⁵ = 32 linhas, e assim por diante.

Aplicações e Curiosidades

• Circuitos lógicos: Na eletrônica digital, tabelas-verdade ajudam a projetar circuitos como portas AND, OR e XOR.
• Validade de argumentos lógicos: Em lógica formal, tabelas-verdade são usadas para verificar se um argumento é válido ou falacioso.
• Explosão combinatória: Para grandes valores de n, o número de linhas cresce rapidamente, tornando impraticável construir tabelas muito grandes manualmente.

Conclusão

As tabelas-verdade são essenciais para entender a lógica proposicional e possuem diversas aplicações práticas. O cálculo do número de linhas é simples, usando a fórmula 2ⁿ, mas sua aplicação pode ser poderosa. Para prática, tente construir tabelas-verdade para proposições com 4 ou mais variáveis e observe como o crescimento exponencial afeta a complexidade da análise.