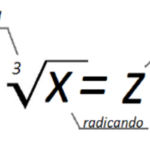Paralelepípedo

O paralelepípedo é um sólido geométrico tridimensional formado por seis faces retangulares. Ele está presente em muitos objetos do dia a dia, como caixas, tijolos e blocos de construção.

Neste artigo, você vai aprender suas principais fórmulas, ver exemplos resolvidos e praticar com exercícios.

---

Características do Paralelepípedo

• Faces: 6 (todas retangulares)

• Arestas: 12

• Vértices: 8

• Quando todas as faces são retângulos, temos o chamado paralelepípedo reto retângulo (o mais comum).

---

Fórmulas do Paralelepípedo

Sejam:

• a = comprimento

• b = largura

• c = altura

🔹 Volume (V):

🔹 Área da Superfície (A):

🔹 Diagonal (d):

---

Exemplos Resolvidos

Exemplo 1 – Volume

Um paralelepípedo tem dimensões a = 5 cm, b = 3 cm e c = 10 cm.
Qual é o volume?

✅ Resposta: O volume é 150 cm³.

---

Exemplo 2 – Área da Superfície

Um paralelepípedo possui a = 4 m, b = 2 m e c = 3 m.
Qual a área total?

✅ Resposta: A área total é 52 m².

---

Exemplo 3 – Diagonal

Um paralelepípedo tem dimensões a = 6 cm, b = 8 cm e c = 24 cm.
Qual é o comprimento da diagonal?

✅ Resposta: A diagonal mede 26 cm.

---

Exercícios Propostos

1. Calcule o volume de um paralelepípedo cujas dimensões são a = 7 cm, b = 4 cm e c = 12 cm.

2. Um paralelepípedo tem dimensões a = 2 m, b = 5 m e c = 9 m. Determine a área da superfície.

3. Encontre a diagonal de um paralelepípedo com a = 10 cm, b = 10 cm e c = 15 cm.

---

Gabarito

1) Volume

✅ Resposta: 336 cm³.

2) Área da Superfície

✅ Resposta: 146 m².

3) Diagonal

✅ Resposta: 5175\sqrt{17}517​ cm (≈ 20,62 cm).

---

Conclusão

O paralelepípedo é um dos sólidos geométricos mais importantes da geometria espacial. Suas fórmulas são simples, mas muito úteis em problemas práticos e escolares.
Dominar o cálculo do volume, área e diagonal é essencial para quem estuda matemática no ensino fundamental e médio.